What are Parallel Lines in Geometry and How are They Constructed?
- muhammadmoazzamamj
- Nov 29, 2024
- 2 min read
Updated: Jun 29, 2025
Parallel Lines are one of the most important concepts in mathematics used widely in different fields of life. Parallel lines are beneficial in fields like engineering and the arts. In this post, we (US ELITE TUTORING) will guide you through the definition and different concepts of parallel lines alongside how they are constructed.
Definition
Two lines in the same plane and not intersecting each other at any point are known as parallel lines. The distance of the lines from each other is constant throughout. The parallel lines are denoted by the symbol "II" e.g. Line AB II CD.
Construction of Parallel Lines
There are several ways we can construct parallel lines and the simplest one is using a ruler. Put it on the page and don't move it now draw straight lines on both sides of the ruler.
The second method is to use a set square with the ruler. First, draw a line on the paper and then now align one of the edges of the line with a set square. Keeping the set square fastened to the ruler, slide it down the line at the proper distance to draw a parallel line "m".

Parallel lines can be constructed by using a compass and protector. Where angles are used to make these lines.
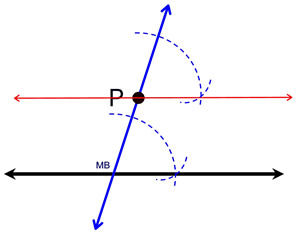
Propertise of Parallel Lines
Parallel lines will have always an equal slope, which means that if a straight line is drawn across both lines the angle will be the same as well.
The exterior and interior angles of the lines are always the same.
The distance between both lines is the same throughout.
The above properties are demonstrated in the figure below:
Applications on Parallel Lines
Parallel Lines are widely used in Architecture and Engineering. For example, in the construction of Bridges where columns can be considered as parallel lines. Besides that, it is vital in the construction of tall buildings.
Parallel Lines are used in Maps and Navigation as travelers and navigators can better understand locations by using the parallel latitude lines on a globe.
These lines are helpful in painting and art designing where sculptures and statues are stabilized and made aesthetic due to parallel lines.
Identifying Parallel Lines
The two common ways to check whether two lines are parallel or not is to check the slope and angles of these lines on different points. For example, mark two points each on both lines draw straight lines intersecting those points, and then check whether the internal and external angles are the same or different. Repeat the same process for the other two points. If the angles are the same it means that the lines are perpendicular. Secondly, check the slope on each point and it should be C1 = C2.
We consider the concept of parallel lines a simple one, but indeed it is a base for many important mathematical topics. Mainly, parallel lines are most important in geometry subject.




Comments