Untangling the Calculus Mysteries
- Areeba Siddiqui
- Aug 16, 2023
- 3 min read
Updated: May 1, 2024

Calculus originally known as infinitesimal calculus, is a mathematical branch of study that focuses on limits, continuity, derivatives, integrals and infinite series. Many counting elements appeared in ancient Greece, then in China and the Middle East, and then again in medieval Europe and India. Infinitesimal calculus was developed independently by Isaac Newton and Gottfried Wilhelm Leibniz at the end of the 17th century.
Calculus is a word that frequently conjures a combination of energy and fear in the hearts of students. This branch of mathematics has empowered mankind to understand and display the complex cycles of progress and movement in our real world. Whether you're an eager numerical devotee or somebody who shudders at the prospect of calculus, we should set out on an excursion to demystify math and investigate its principal ideas. It has two significant branches; differential calculus and integral calculus.
Calculus is been narrowed down to further subdivisions by stepwise revelation;
Foundation:
At the core of calculus lies the idea of limits. Envision following the movement of an article as it speeds up or dials back. To comprehend its momentary speed, you really want to look at its movement at increasingly small time spans. This is where limit become an integral factor - they permit us to grasp how a point acts as it moves toward a specific point of destination. This idea is vital for laying out the foundations of calculus and examining persistent functions, where no abrupt leaps or breaks exist.
Differentiation:
Differentiation is in many cases thought about the lead idea of calculus. It empowers us to work out paces of progress and comprehend how a function behaves. Consider a winding street - its incline changes at each point. Essentially, in math, differentiation estimates the pace of progress of a function at some random point. This is especially valuable in fields like physics, designing, and financial aspects, where understanding how variables change is fundamental.
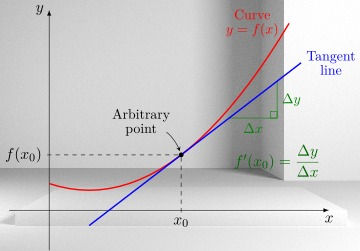
Integration:
Integration, the kin of differentiation, fills an alternate need. It assists us with tracking down the gathered amount or region under a curve. Envision plotting the speed of a moving vehicle on a chart. Coordinating this curve gives you the distance the vehicle has voyaged. In certifiable situations, coordination helps with working out regions, volumes, and even probabilities.
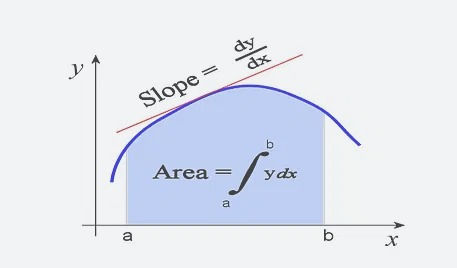
Fundamental Theory of Calculus:
The major hypothesis of Calculus flawlessly integrates differentiation and integration. It expresses that differentiation and integration are inverse operations of each other. In less complex terms, while differentiation gives the pace of progress of a function, integration uncovers the first function itself. This hypothesis supports many high level ideas in calculus and exhibits its binding together power.
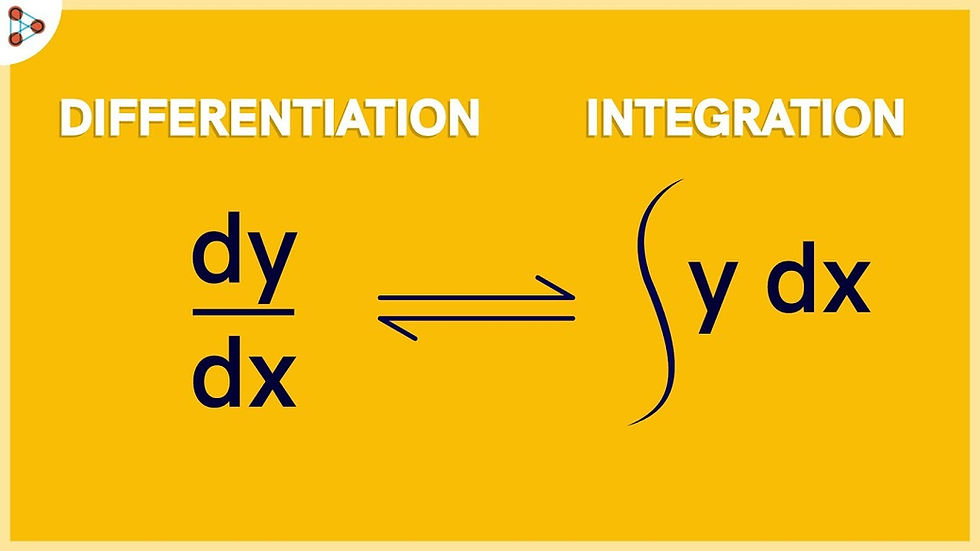
It's Implications:
Calculus could appear to be conceptual, however its certifiable applications are immense and various. Physics depends on calculus to portray the movement of articles, anticipate divine peculiarities, and plan the laws of nature. Engineering utilizes calculus to configurate structures, advance cycles, and investigate frameworks. Financial and economic matters benefits from calculus to demonstrate monetary development, anticipate market drifts, and upgrade asset portion.
Edition; Multivariable Calculus:
As we adventure into a multi-layered universe, we experience multivariable calculus. In this domain, we investigate functions with various inputs and outputs, urgent for figuring out complex frameworks. It finds applications in fields like PC designs, fluid dynamics, and even machine learning algorithms.
Beyond Infinity:
Calculus isn't bound to the limited world. It digs into the endless domain with arrangements and series. Consider including a limitless number of numbers - appears stunning, isn't that so? Calculus prepares us to handle these limitless aggregates, offering insights into numerical examples and approximations that support present day innovation.
Conclusion:
Generally, Calculus is undeniably beyond the set of equations to be solved; a language empowers us to unravel the powerful texture of our reality. From understanding the universe's crucial laws to making state of the art innovation, calculus engages us to reveal the secrets of change and motion. In this way, whether you're an aspiring mathematician or basically inquisitive about the powers molding our world, embrace the excursion of unraveling calculus - it's a fare to the journey of exploring heart of the mathematics..




Comments